資產配置致勝關鍵
日期:2012-02-18
資產配置最關鍵的因素就是兩組資產的相關係數,只要選擇到正確的投資標的組合,不用任何波段操作,只要持有就可以降低投資標的之波動度。什麼是對的組合呢?重點就是如何找出關聯度愈低愈好的兩組資產,甚至是具有反面走向特質的兩組資產,也就是統計學上的負相關,將兩組配起來就好了。基本原理是當兩組資產沒有關聯,就會有「機會」當一組資產的報酬率高於平均值時,另一組資產是低於平均值的。將這兩組資產「相配」起來,總報酬率會得到平均值,但是總波動度卻會比個別波動的加權平均還要低。
資產相關聯的程度是以相關係數衡量,相關係數愈低,波動度就愈低,若是完全的負相關,理論上還可以配出零波動風險的資產組合呢!然而這些都需要統計學的基礎,一般的讀者會較為卻步,相信透過模擬的方式,可以讓資產配置簡單的呈現。前半段不免俗的先簡單解釋資產配置的理論基礎,而後半段提供一個Excel試算檔供讀者下載,透過模擬來學習資產配置精髓,資產配置就不會再那麼艱深難懂了。
波動度以標準差衡量
股票或債券等資產的報酬率是每年都會在平均報酬率上上下下波動,而且是呈現自然分配。波動的程度可以透過標準差來衡量。標準差愈大,代表波動就愈大。標準差愈小,代表波動就愈小。標準差為零時,就是沒有波動風險。
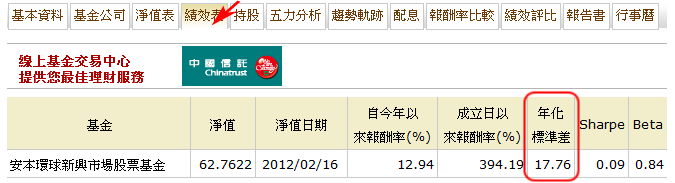
標準差的資料在各大財經網站都可以找得到,例如晨星(Morningstar)或MoneyDJ網站都可以找得到。下圖是MoneyDJ網站上的安本環球新興市場股票型基金的年化標準差,可以看出來是17.76%,要記得點選「績效表」才有這資料。
資產組合後的報酬率是加權平均
兩組資產經過組合後,整組資產的平均報酬率是個別資產平均報酬率的加權平均。
例如有一資產配置,由下列兩種基金組合而成,其平均報酬率及標準差分別如下:
- 股票型基金:平均報酬率為15%、標準差為20%
- 債券型基金:平均報酬率為6.5%、標準差為3.5%
若股票型基金及債券型基金各佔一半,那麼這組基金的總報酬是加權平均報酬:
=15%*0.5 + 6.5%*0.5
= 10.8%
資產組合後的波動度由相關係數決定
不過組合後的標準差並非個別標準差的加權平均,而是會比加權平均還要低。例如上面例子,標準差的加權平均為11.75% (=20%*0.5 + 3.5%*0.5),那麼組合後的標準差一定比 11.75% 還要少,至於會少多少卻是由兩組之間的相關係數來決定。相關係數愈低,就愈小於11.75%。
組合後標準差公式
組合後的標準差 σp 公式 1 所示,可以看出跟兩組資產個別的投入比例(w1, w2)、各別標準差(σ1, σ2)以及兩者之間的相關係數 ρ 有關係。
![]() ----------
公式 1
----------
公式 1
不同相關係數下的簡化公式
相關係數 = 1
當ρ 等於 1 時,也就是兩者是絕對的正相關,就是當一組資產的報酬比平均值高時,另一組資產也一定比平均值高。那麼將公式 1 的 ρ 用 1 代入,就可以變成如下列公式 2。可以看出這就是兩個個別標準差之加權平均,也就是兩種資產相互配置起來最差的狀況。所以說,兩個絕對正相關的配置一點意義都沒有。
![]() ----------
公式 2
----------
公式 2
相關係數 = 0
當ρ 等於 0 時,也就是兩者是零相關,意思是這兩組資產並沒有關連性。也就是有一半的機會當一組資產的報酬比平均值高時,另一組資產會比平均值低。那麼將公式 1 的 ρ 用 0 代入就成為下列的公式 3 。跟絕對正相關(ρ = 1) 相比,可以看出少了中間 2*w1*w2*σ1*σ2這一項,所以說標準差會比相關係數等於 1 的時候還要少。
![]() ----------
公式 3
----------
公式 3
相關係數 = -1
當ρ 等於 -1 時,也就是兩者是絕對的負相關,就是當一組資產的報酬比平均值高時,另一組資產一定比平均值低,在這種狀況下,整組資產的標準差就變成如公式 4 所示。仔細看這兩組資產相配後的標準差是加權後相減的。這意味著如果將比例調整的好,有可能得到波動度為零的資產,也就是沒有波動風險的資產。沒有錯,只要 w1/w2 = σ2/σ1,這組資產的標準差就會等於零。不過讀者不要太高興啦,這條件是兩組資產是絕對負相關(ρ = -1),這在現實中是不可能的。
![]() ---------
公式 4
---------
公式 4
相關程度愈低,波動度就低
由上面公式的演練中,可以看出兩種資產配置後,其平均報酬率是兩組資產的加權平均。然而配置後的標準差卻會比個別標準差的加權平均還要少,會減少多少是跟相關係數有絕對關係。相關係數是負1 到正1之間的小數,正 1 代表兩者絕對正相關,是資產配置最不希望看到的,理由是絕對正相關是一個基金為正報酬時,另一個也一定會是正報酬,所以完全沒有一正一負相互抵銷的「機會」。相關係數 0 代表兩者完全不相關,配出來結果算是不錯的,因為兩組資產的表現完全分開,所以有一半的機會是當一組高於平均時,另一個卻低於平均。組合後的資產波動度就會有一半的機會相互抵銷掉與平均值的波動。相關係數 -1 代表兩者絕對負相關,就是當一個高於平均,另一個「一定」低於平均。所以說相關係數是決定資產配置中最重要的因素,兩者相關的程度愈低愈好,當然最好莫過於負相關了。
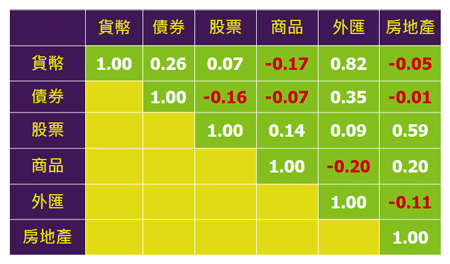
下圖是觀察歷史資料,顯示不同資產之間的相關係數:
資產配置模擬
若是只有理論的公式,想要吸收當中的道理會比較困難,這裡提供一個Excel試算表,可以模擬資產配置狀況。因為一組資產的報酬率是每年變動的且呈現自然分配,所以使用隨機變數來模擬。只要風險性資產呈現自然分配,當然就可以透過平均報酬率及標準差(μ , σ)兩個參數來描述,所以試算表中讓使用者可以自行設定兩組不同資產的平均報酬率及標準差(μ1, σ1, μ2, σ2),以及這兩組資產之間的相關係數( ρ )。借由調整相關係數,就可以看出兩組資產組合的變化。
下載Excel試算表
點選Excel圖示可以下載Excel試算表。
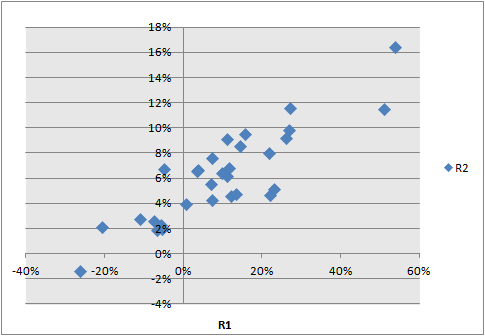
B1儲存格(w1)是投資第一組資產的比例,必須介於0~1的數值,讀者可以自行調整。B2儲存格(w2)是投資第二組資產的比例,因為只有兩組資產,所以第二組資產的比例一定是 1 減去第一組資產的比例,當然這儲存格屬於公式,不可以調整。表格中R1欄位是根據第一組資產所設定的平均值及標準差所產生的隨機變數,R2欄位是根據第二組資產所設定的平均值及標準差所產生的隨機變數,而且R1、R2這兩組隨機變數具有B7儲存格所設定的相關係數之特質。R1及R2的相關性可以由散布圖中看出來,下圖是相關係數為0.85的圖型。
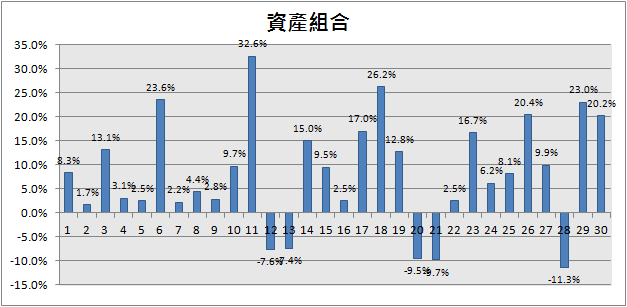
其實投資者真正關心的是兩組資產在不同相關係數的情況下,組合後的投資報酬率會是如何。「資產組合」欄位是兩組資產在(w1, w2)的比例下,組合後的投資報酬率是多少。下圖是w1=0.5, w2=0.5, μ1=15%, σ1=20%, μ2=6.5%, σ2=3.5%, ρ = 0 的條件下的結果。此試算表模擬30年,每一長條代表該年度的投資報酬率。
零風險情況
當相關係數為 -1 時,只要 w1/w2 = σ2/σ1,就可以得到零風險的投資組合,而且投資報酬率維持在加權平均。雖說這實務上是不可能,不過透過模擬來完成,也是一件有趣的事。因為w1+w2=1,而且 w1/w2 = σ2/σ1,所以只要在B1儲存格(w1) 輸入公式 = σ2 /(σ1 + σ2),以及B7儲存格(ρ) 輸入-1,就可以看到資產組合的報酬率全部都是平的,一點波動都沒有,而且固定在組合後報酬率(B8儲存格)。






