複利次數對利率有何影響
日期:2007-06-08
一般我們在銀行這些金融機構,會看到標示的利率,可是常常不論是存款或貸款,當銀行對帳單來的時候,所算出來的金額又跟我們想像的不一樣。主要是因為銀行所標示的是名目利率(Nominal Interest Rate),是未考慮複利效應的一種利率標示方式。當把複利因素考慮進來後,實質所得的利率稱之為有效利率(Effective Interest Rate)。
一般投資者都知道複利具有強大的威力,是投資理財致富的主要關鍵,可是常常誤以為每年複利次數愈高,期末金額會有巨大的變化,也就是相當於有效利率會大幅上升。所以常聽到有人說,地下銀行是以日計息,那利息可是會嚇死人的。然而事實剛好相反,複利次數高到某種程度後,有效利率便會停滯不前了。地下銀行可怕之處是因為高的嚇人的名目利率,並非每日複利的結果。有效利率和每年複利的次數有關,複利次數愈多次,期末本利和當然愈高,但是次數高到某種程度後,有效利率成長就遲緩,而不再升高了。
複利的意義是本金經過一段時間後,會產生利息,再將所孳生出來的利息加入本金,上期的本金加上所產生的利息稱為本利和,將本利和當作下一期的本金繼續生息,便稱為複利。那就有一個問題產生了,這一段時間到底是多久?亦就是多久會結算利息一次,來併入下期的本金計息,簡單說就是多久複利一次。我們不用多加思考也知道,對存錢者來說,一年複利愈多次愈好囉。那麼是半年複利一次,還是每季、每月、每日、每小時還是每分呢?之間的差別是什麼呢?不同的複利期間對有效利率的影響是多少,就是本文探討的重點。
名目利率(Rn)
名目利率(Nominal Interest Rate)是一年計息一次的年利率,這利率並未考慮一年複利幾次的利率,一般的金融機構都是以名目利率標示的。
每月複利一次的有效利率
有效利率指的是每年經過一定次數的複利後,將實際上所產生的利息除以本金的等值利率。例如銀行在實務上,利息是每月結算一次,結算後的利息會加入本金來計算,所以銀行的複利期間是一個月。我們可以利用終值公式來導出每月複利一次的有效利率,終值(FV)的公式如下:
FV = A*(1 + r)m ;A = 本金,r = 每期利率,m = 期數
如果名目利率Rn,每月為一期,所以每期利率(月利率) r = Rn / 12,一年後經過12期的複利效果會得到終值
FV = A*(1 + Rn / 12)12,利息所得是將12月後的終值減去期初本金A:
利息 :
= FV – A
= A*(1 + Rn / 12)12 – A
= A * ((1 + Rn / 12)12 – 1)
有效利率(Re) :
= 利息 / 本金
= A * ((1 + Rn / 12)12 – 1) / A
= ((1 + Rn / 12)12 – 1
所以Re = (1 + Rn / 12)12 – 1,這個利率是經過12月的複利後,所得到的有效利率Re。這利率的真正意思是說,雖然銀行掛牌利率為Rn,但是如果存一年(12個月)的話,經過12個月的複利後,經換算銀行實際付給你的利率等於Re = (1 + Rn / 12)12 – 1,那麼一年後拿到的利息 = 本金 * Re。
例如存100元定存,名目利率5%,經過12個月複利後本利和 = 100*(1+5%/12)^12 =
105.1162,減去本金100元後得利息5.1162元,所以:
有效利率 = 5.1162 / 100 = 5.1162%。
直接用公式計算
Re = (1 + R/12)12 – 1
= (1+5%/12)^12 -1
= 5.1162%
有效利率之公式
如果每年不是每月複利一次,可能是每季複利一次,那又該如何算呢?有效利率可以寫成下列通式:
Re = (1 + Rn / m)m – 1,m 等於每年複利的次數
| 複利期間 | 每年複利 次數(m) |
有效利率(Re) 公式 |
有效利率(Re) 範例 名目利率Rn = 6% |
| 季複利 | 4 | =(1 + Rn / 4)4 – 1 | =(1+6%/4)^4-1 = 6.136% |
| 月複利 | 12 | =(1 + Rn / 12)12 – 1 | =(1+6%/12)^12-1 = 6.168% |
| 日複利 | 365 | =(1 + Rn / 365)365 – 1 | =(1+6%/365)^365-1 = 6.183% |
以上表最右方欄,名目利率6%為例,我們可以看到當每年複利次數愈多時,有效利率是會往上爬升,但不是呈現線性往上走,而是趨近於6.183%就不再往上走了。每月複利一次的有效利率是6.168%,和名目利率6%相差了0.168%。可是日複利的有效利率是6.183%,和月複利的有效利率6.168%僅相差0.015%,可見每年複利次數愈多,相差就愈少了。下圖就可以很清楚看得到複利次數和有效利率的關係了,當每年複利次數增加時,有效利率的增加率就減少了,最後停在6.183%,亦就是連續複利的有效利率。
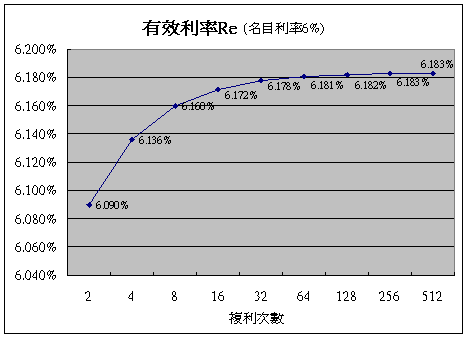
連續複利
有效利率公式是Re = (1 + Rn / m)m – 1,如果m 等於無窮大時,可以視為隨時都在複利,亦就是連續複利,當m趨近無窮大時,根據自然指數定義 (1 + Rn / m)m 等於 eRn,所以有效利率Re = eRn – 1。例如當名目利率為6%時,連續複利時的有效利率等於 e6%-1,可利用excel來算 = exp(6%)-1 = 6.18365465453596%,亦就是說名目利率6%,隨著每年複利次數的增加,有效利率會往上增加,但是次數越高增加愈少,到最後達到約6.183655%。
Excel試算
結論
每年複利次數對有效利率雖有影響,但是影響不大,那為什麼複利的威力會那麼大呢?複利的意思是:本金每年會以(1 + 有效利率)的倍數成長,而決定有效利率的主要因素是名目利率,所以名目利率大小,以及投資年數才是真正會影響投資理財的最大因素。






