資產配置-實例篇
日期:2008-04-27
在網站裡也談了許多關於資產配置的理論,但是總覺得少了些較具有說服力的範例。這一次直接下載富達網站的歐洲基金及美元債券型基金的淨值資料,日期涵蓋自1991年到現在為止。用這實際的回流測試來告訴大家,真的,理財就是這麼簡單!做好資產配置後,基金買來就放著,固定時間調整一下就好了。
回流測試
當我們想知道一個投資方式是否有效時,最好的方式就是利用回流測試,假設時間倒退幾年,然後用這方法投資,再利用實際發生的數字,驗證該投資是否如預期般的有效。所以我也是利用回流測試的方法來說明資產配置理論,作法分成三個階段:
- 選定資產標的及取得歷史資訊
- 將時光倒回,依實際發生狀況演練
- 分析及比較結果
這裡有一份Excel檔案,就是回流測試的結果,下面章節會詳述這份檔案的製作方式。
下載Excel檔案
第一步:選定資產標的及取得歷史資訊
這次實際演練標的是選擇富達歐洲股票型基金及富達美元債券基金,主要因為兩組基金一個是股票另一個是債券,比較可說明股債平衡的道理。那為什麼又是富達基金呢?主要原因只是資料取得容易,目前網路上能取得多年淨值資料的也只有富達基金。這階段的做法如下:
1.取得所選取基金之每月淨值資料
2.個別算出兩組基金的每月報酬率
3.求得兩組基金月報酬率的平均值(μ)及標準差(σ)
4.算出兩組基金月報酬率的相關係數(ρ)
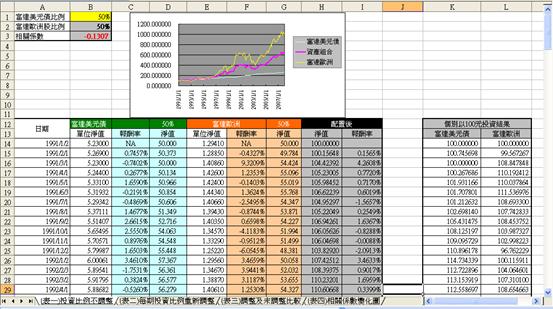
先看Excel的工作表:(表一)投資比例不調整:
位置 |
意義及公式 |
| B欄 | 富達美元債的每月淨值表 |
| C欄 | 富達美元債每月報酬率 月報酬率的公式如下:(當月淨值 – 前月淨值) / 前月淨值 |
| C218 | 富達美元債的月報酬率平均值(μ),以average函數計算。 |
| C219 | 富達美元債的月報酬率標準差(σ),以stdev函數計算。 |
| E欄 | 富達歐洲基金的每月淨值表 |
| F欄 | 富達歐洲基金每月報酬率 月報酬率的公式如下: (當月淨值 – 前月淨值) / 前月淨值 |
| F218 | 富達歐洲的月報酬率平均值(μ),以average函數計算。 |
| F219 | 富達歐洲的月報酬率標準差(σ),以stdev函數計算。 |
| B3 | 富達美元債及富達歐洲的月報酬率相關係數(ρ),以correl函數計算。 |
第二步:時光倒回,依實際發生狀況演練
基本資料做完後,接著就是將時光倒轉至1991年,然後拿出100元,分別以50元投資富達歐洲基金,50元投資富達美元債券基金。然後假設“買入長期持有”,我們來看看這兩支基金的淨值會是如何變化。然後把兩支基金的月淨值相加,就會得到配置後的淨值了。根據配置後的淨值,就可算出月報酬率及其平均值和標準差。
位置 |
意義及公式 |
| D欄 | 富達美元債,在1991年1月投入50元後的每月淨值。 |
| G欄 | 富達歐洲,在1991年1月投入50元後的每月淨值。 |
| H欄 | 富達美元債的月淨值 +富達歐洲的月淨值 這欄就是配置後的淨值 |
| I欄 | 根據H欄淨值算出的月報酬率,也就是配置後的月報酬率 |
| I218 | 配置後的月報酬率平均值 |
| I219 | 配置後的月報酬率標準差 |
第三步:分析及比較結果
當回流資料做好後,接著就是分析及比較的工作。最好的方式就是將配置前及配置後相互比較,這樣最為清楚。我們已經有了兩基金配置後的淨值,及月報酬率。但是要比較的話,兩者比較基礎必須一樣,亦就是每基金個別於期初也投入100元,看看結果是如何:K欄是單獨富達美元債的結果,而L欄是單獨富達歐洲的結果。而H欄就是配置後的結果。下圖就是H、K、L欄的資料以圖表呈現的結果。黃線是富達歐洲,淺藍線是富達美元債,粉紅色是兩者配置結果。可以清楚看到,配置後的淨值是穩定多了,淨值波動介於兩者之間。
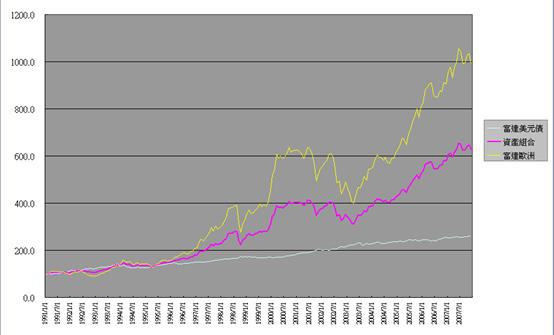
光是看了這結果是不夠的,還得跟理論值確認看看是否一致。
| 項目 | 平均值(μ) | 標準差(σ) | |
| 富達美元債 | 0.4862% |
1.1965% |
|
| 富達歐洲 | 1.2539% |
4.8274% |
|
| 兩者配置後 | 實際值 | 0.9605% |
3.1953% |
| 理論值 | 0.8701% |
2.4096% |
|
上表的理論值是根據下列公式計算出來:
A資產平均報酬率為μa 標準差為σa 佔總資產比例wa
B資產平均報酬率為μb 標準差為σb 佔總資產比例wb
AB資產相關係數:ρab
配置後:
平均報酬率 = wa*μa + wb*μb
= 0.5*0.4862% + 0.5*1.2539%
= 0.8701%
標準差 = ![]()
=((0.5*1.1965%)^2+(0.5*4.8274%)^2+2*(-0.1307)* 0.5*1.1965%*0.5*4.8274%)^0.5
= 2.4096%
奇怪,為何和理論值不合
由上表中可以看出配置後的結果和理論值是有所差距的,我們預期平均報酬率應該是0.8701%及標準差2.4096%,可是配置結果卻得到0.9605%的平均值及3.1953%的標準差。雖然平均報酬率比預期高但是標準差也比理論值高了。怎會理論值和實際做法會有差距呢?如果不解決這問題,如何直接由理論值來推論結果呢。還好這問題發生在配置的比例上,因為理論值是根據兩者比例是50/50所計算出來的,可是實際的配置只有在期初是50/50,經過第1個月以後,兩者淨值比例分配就不再一樣了,而且時間愈長,比例偏差就愈大了。
把這問題解決後,看是否跟理論值會完全一樣!Excel的工作表“(表二)每期投資比例重新調整”,就是將每月的投資金額,按照上期的期末配置後淨值重新分配比例,得到結果就和理論值完全一模一樣了。下圖(Excel工作表三)是每月的投資金額經過調整及未調整的比較圖:
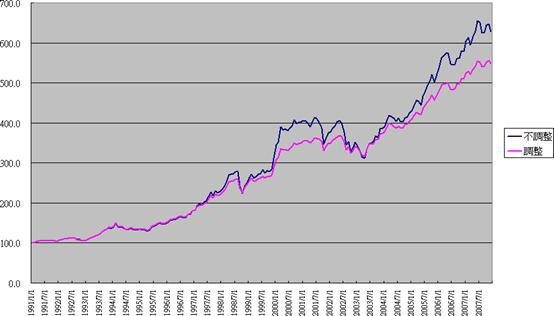
可以看出調整過後淨值波動會比較平坦,但是最後表現會略差。這是符合預期的,標準差(波動)大幅減少,但是平均值較差,這跟計算出來是完全一致的。
那麼該多久調整一次
如果一開始設定一個分配比例,但是隨著時間拉長這比例就會跟著變,但是實務上並不必要每月調整,因為調整比例是得付出成本的,只有當比例大到非我們預期時,再來調整即可。個人投資者只要知道原理,比例上並非要求那麼精準,差一些是沒多少影響的。Excel之所以會有調整這工作表,是因為要讓讀著知道資產配置理論的正確性,及其變化而已,並非一定得這麼做。
波動變小不只因為股票比例少
有讀者或許會問,股票的成分只剩50%比例變小了,當然波動就會減少了,這有何了不起,還動用了那麼多的統計數學。沒錯!當股票成分變少了,整組配置的標準差本來就會變小,但是如果不是因為負相關的原因,是不會變得那麼小的。我們來看看如果沒有相關係數的因素,單純只是比例因素,兩者組合後的標準差等於多少?只要將兩個基金標準差加起來除以2就是了:
=1.1965%*0.5+4.8274%*0.5
= 3.012%
亦就是說不只單純是因為股票的比例少了的原因,才讓波動減低。因為負相關的原因,讓波動由3.012%降至2.4095%。幅度降了將近20%。
關鍵因素:相關係數(Correlation)
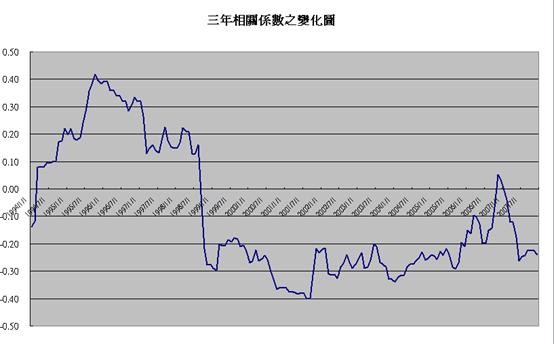
表一及表二的B3儲存格顯示這兩組基金自1991年到現在的相關係數是-0.1307,代表這兩組基金長期呈現負相關。為了感受一下負相關的意義,下圖是隨便抽取前幾個月的報酬率來看看,可以看出大部分時間都是一正一負的,不負相關也難!
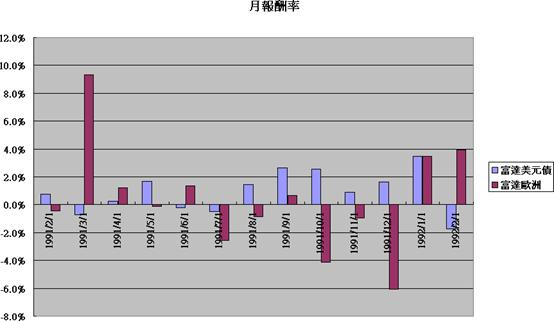
相關係數時間變化
已經知道長時間來看(1991年到2007年),這一組基金是呈現負相關。可是在任何時刻都一樣嗎?既然資料都已齊全,反正用Excel做也非常容易,也就“順便”看看吧!在Excel的(表二)L欄,是兩組基金的“當時”相關係數,L欄的每一儲存格,是以那個月為基準用前三年的資料所計算的相關係數。可以解讀成那期間的相關係數。下圖(表四)就是將L欄的當時相關係數隨著時間變化圖。可以看出2007年以前都是呈現約-0.3的負相關,只有在1994~1999年是正相關的。雖然那時期是正相關,但是平均也大約0.25左右。這張圖說明了,這兩支基金的配置應該是很不錯的。
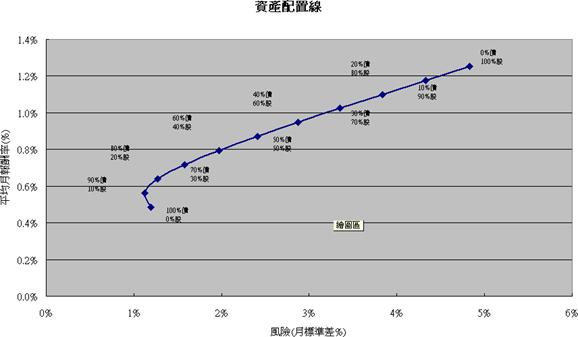
資產配置線
表一及表二的B1儲存格讀者可以自行調整富達美元債券的比例,目前預設值是50%。當比例調整時,可以觀察該工作表最上面的淨值圖,觀察配置後的結果(粉紅色的線),在不同的比例配置時的變化情形。
除了一個一個的看配置後淨值曲線,還可以一次看10種配置的結果:表五的資產配置線。裡面的值是將B1比例,由0%調整到100%,每次調整10%,然後一一將配置後的平均值及標準差紀錄下來。下圖最左邊的那一點是100%的美元債0%歐洲股,每往右上一點增加10%歐洲股,減少10%美元債。直到最右邊一點是百分之百的歐洲股。
資料下載
這篇文章所用的基金資料是由富達網站所下載的,進入網站後,有三個欄位讓你選擇基金資料,如圖所示就可選到本文所用的範例。

選擇好基金後,按確定便進入歷史淨值的頁面。在該頁的最下面有“下載淨值檔案”(如下圖),選擇Excel檔案,就可以下載歷史淨值了。淨值下載後是以日為單位的淨值,然而我們希望是每月的淨值,可以在淨值欄旁邊取另一欄作為標示(例如D欄),於D欄裡一個儲存格(例如D12)置入以下公式=IF(MONTH(A12)=MONTH(A11)," ","Y"),在將這公式複製到D欄其他儲存格。每月的第一天的儲存格就會出現”Y”,其他只會出現空格。再利用篩選功能過濾出只顯示有”Y”的列就可以了。







