讓退休金永遠花不完的公式
日期:2011-12-01
如果有一筆退休金,不論年紀多大都永遠花不完,而且還可傳給後代,那該有多好!不要以為這得要很大的一筆錢才可以辦得到。其實不然,所需金額甚至比一般人所規畫的退休金都還要來得少。
記得在退休以前跟一位同事討論退休金得準備多少金額才夠,結果那位同事說要2,560萬才夠。我有些訝異為何需要那麼多?便請他算給我看。原來他們夫妻兩人,希望退休以後可以維持每年80萬的生活品質。當時的年紀50歲,若以平均餘命82歲來計算,還有32年要活,所以說總計需要2,560萬元。
這樣的算法讓我有些替他擔心,首先是沒有考量到通貨膨漲率的問題,也就是10年、20年後的80萬,將不再只是80萬,而是比80萬多很多的數目。然而更要命的是,這位仁兄竟然以平均餘命來計算退休需求年數。萬一自己比較幸運,活得比82歲還要久,那以後的生活費又該如何是好!平均餘命同時也意味著有不少的機會,會活得比平均餘命還要久,光是從馬路上或公園所看到的老年人數目,就可以知道了。
通貨膨漲率的問題較好解決,只要把每年通貨膨漲率考慮進來,全部加總也就解決了。倒是該準備多少年的生活費,相信沒有人說得準,因為沒有人可以預測自己會活多久!
利用永續年金的觀念
有一種規劃退休金的方法,可以同時考慮通貨膨漲率,而且跟需求年數無關。因為可以用單筆金額的退休金,就可以創造出未來無限多筆的現金流量(如下圖),使得退休金永遠都花不完。其實就是利用永續年金的觀念:無限多筆的現金流量(L),當投資報酬率為R時,其現值等於L/R。

現值的意義用白話文來說明,就是未來無限多筆的生活費用(L),其現值加總“等於”現在單筆的退休金(L/R)。讀者不需要了解這數學如何證明,只要抓住觀念即可。這當中的道理很簡單,只要退休金每年所產生的報酬,比每年所需要的生活費還要多,這樣本金就會愈來愈多,當然報酬也是愈來愈多囉。
以我同事的例子來說明就更清楚了,不過為了簡化問題先不考慮通貨膨漲。每年需要80萬元的生活費,若將退休金投入平均報酬率10%的標的,那麼只要準備800萬元的退休金就綽綽有餘,而且永遠花不完。不要懷疑,你沒有看錯!只要800萬,就可以創造出未來無限多的80萬,直到永遠。
這是因為10%的投資報酬率,以800萬的本金,第一年底就可以創造出80萬元的獲利,那麼年底本金加獲利就有880萬元,這時將80萬元生活費提走,第二年初的本金依然還剩800萬元。既然本金沒有短少,第二年當然還可以維持80萬元的獲利,同樣的再提出生活費80萬之後,本金還是維持800萬元不變。依此類推,不論經過多少年,每年提出80萬之後,800萬的本金永遠一毛都不會減少。說得誇張一些,當你身故後這本金依然維持,還可以留給下一代,世世代代永遠花不完。
這800萬又是如何算出來的?就是永續年金的公式:
退休金 = 每年生活費(L) / 投資報酬率(R)
例如每年生活費80萬,投資報酬率10%,那麼退休金等於800萬(=800,000/10%)
不過通貨膨漲是生活現實,就必須考慮進去。這時公式就得修正如下:
退休金 = 每年生活費 / (投資報酬率 - 通貨膨漲率)
在通貨膨漲率為2%的情況下,投資報酬率10%,退休金就得準備1,000萬,才可以永遠花不完:
=800000/(10%-2%)
=10,000,000
報酬率愈高、所需要退休金愈少
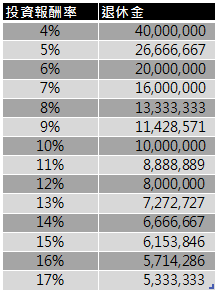
以上公式說明了這樣所規畫的退休金,跟投資報酬率息息相關,下表列出了不同的投資報酬率所需要的退休金,條件是每年生活費80萬,通貨膨漲率2%。從表中很清楚的看出來,投資報酬率扮演著相當非常重要的角色,當投資報酬率10%,只需要1,000萬元退休金;若投資報酬率只有4%,就得準備4,000萬才夠。也就是投資報酬率愈高,所需要的退休金額就愈少。
既然投資報酬率那麼重要,當然就得將投資報酬率盡可能的拉高,只是愈高的投資報酬率所伴隨而來的就是波動度的增高,這時資產配置就更顯重要了。退休金的資產配置我建議70%債券型基金,30%股票型基金。債券型基金平均報酬率6.5%,股票型基金12%來計算,資產配置後的平均報酬率等於8.2% (=6.5%*0.7+12%*0.3)。在這樣的配置下,只要擁有1,290萬,退休金就永遠都用不完。
=800000/(8.2%-2%)
=12,903,226
不管多年輕都可以退休
以這種方式所規劃的退休金,除了可以讓退休金永遠花不完之外,還可以讓你提早退休。因為這種退休金的方式永遠用不完,所以不論年紀多年輕,只要累積到所規劃的金額,就具備退休條件。當然我並不鼓勵年輕人提早退休,但是較早達到財務自由,可以早點不為五斗米折腰,做自己想做的事,這樣的人生不是很美好嗎。
本文刊登於Smart智富月刊160期







