72這數字如何算出來的
日期:2013-12-16
72法則是整個複利的關鍵,只要將72除上投資報酬率,就可以得到資產以複利翻一倍所需的年數。許多人都知道72法則,但卻不清楚72這數字是如何得來的。其實72這數字並非精算出來,這只是從經驗中得出的一個概數而已,但實用性也非常夠了。
要精算投資翻一倍所需要的年數,可以用Excel的NPER函數來計算,公式如下:
=NPER(年報酬率, 0, -1, 2)
例如年報酬率為8%,那麼資產要翻一倍所需要的年數就是9年[=NPER(8%,0,-1,2)],以這公式做了一個表格,列出不同的年報酬率,翻一倍所需要的年數,以及這兩個數字的乘積再乘上100 (最右邊欄位)。
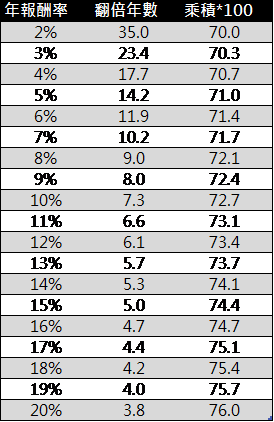
這表格列出2%到20%之間的報酬率,這也是大部分投資的落點,可以發現最右邊一欄的數字變化不大,幾乎都落在70~76之間。如果要精確的計算,就不應該使用72當被除數,每個報酬率都必須使用相對應的數字來除上報酬率才正確,例如15%就應該使用74.4而不是用72。但這就太不方便了,72只不過為了方便心算,取個中間數字而已。全部都用72來代替的話,誤差也不會相差太多。
就以誤差最大的2%及20%這兩個報酬率來說,若報酬率為2%,精算翻倍年數為35年,但用72法則來算結果是需要36年,兩者只不過差了一年。當報酬率為20%,精算出來的3.8年就可以翻一倍,同樣用72法則算只需要3.6年,只差了0.2年。以這樣的些微的誤差,實務上已經相當夠用了。
72法則主要是讓投資者評估一項資產,利用複利成長,需要多就可以成長一倍。例如投入100萬資產於投資報酬率15%的資產,可以輕易算出只要4.8年,就可以成長到200萬。同樣的,如果有1,000萬也是4.8年會翻一倍至2,000萬。複利的關鍵,在於如何有效的縮短資產翻倍所需要的年數。只要翻倍的年數可以縮短到6年,那麼36年的期間就可以翻6次。如果有100萬,翻一次為200萬,再翻一次為400萬,依此類推翻了6次,結果可以成長64倍(26),也就是6,400萬。所以說,複利的關鍵再於如何縮短翻倍所需要的時間,讓我們在有生之年可以翻愈多次。






