資產配置-相關係數篇
日期:2008-04-23
在基金公司的宣傳裡,常看到『股債平衡』這個廣告詞。最近在富達投資的網站裡,看到一份不錯的資產配置文章,想提出來跟大家分享。只是這篇文章是以英文書寫,但我不打算逐一翻譯,想用“看圖識字”的方式再加上我自己的說明來解釋這篇文章。
原文內容:Asset Allocation Report: Stock-Bond Mix Now As Important As Ever。我把這標題翻譯成『資產配置報告:股票-債券之配置仍然如以往一樣的重要』。
資產配置理論
想看懂這篇文章得先對資產配置的理論有一些了解。所謂資產配置(Asset
Allocation)就是將兩者以上的資產以不同的比例混合起來,來達到分散風險的目的。一般資產配置的分散風險所舉的例子,通常是不要把雞蛋通通放在一個籃子裡。但是資產配置的分散風險,所表達的是裡面更深一層的意義:資產淨值波動的減低。
資產組合有一項最主要的風險稱為『波動風險』。例如股票、債券或這些證券的基金,淨值是會隨著時間變化的,而且經常是在平均報酬率上上下下的波動。透過良好的混合方式,可以有效的減低整體的波動程度,這種配合的方式就稱為資產配置。內容主要討論比例如何分配,以及如何選擇資產種類,相互之間的組合可以得到減低風險的結果。
相關係數
或許覺得奇怪,就只是選擇資產種類,然後把它配合起來就可以了,難道不用看趨勢、不用研究線型。是的,那些通通不需要!不要懷疑,就是這麼簡單,只要選對資產,然後單純靠著相互的波動,就可以達到這效果。
那為什麼只是兩個資產的組合,就可以減低波動呢?主要的方法就是利用兩組資產的不相關性或者是負相關,來相互抵銷上下的波動。例如有兩組資產:股票基金及債券基金。為了解釋方便假設兩組基金的上下起伏是沒關連的,行話稱為“相關係數為0”。因為兩組基金相互沒關連,所以兩組基金的漲跌是獨立的,也就是口語常說的“你漲你的,跟我可沒關連喔”。雖然說兩組互不相關,但總會有一些機會是『恰巧』股票基金漲,而債券基金跌;或者是股票基金跌,債券基金漲。這些時候兩組基金的波動不就會相互抵銷了。資產配置說穿了就是靠著這『恰巧』兩字。『恰巧』的機會多,相互抵銷的部份就多;『恰巧』的機會少,相互抵銷的部份就少。
如果我們選擇另外兩組基金,全部都是美國的股票型基金,一個稱為A基金、另一個稱為B基金。亦假設這A、B基金是完全正相關,行話稱為“相關係數為+1”。因為兩組完全相關所以兩基金等於是連動的,也就是說A基金漲,B基金也一定漲,同時漲幅都一樣。而且當A基金跌時,B基金也一定跌。這樣的組合是不可能降低任何波動的,因為一點點『恰巧』“一正一負”相互抵銷的機會都沒有。
接下來我們再來看有沒有那兩組資產或基金是反方向關聯的,就是所謂的負相關。假設極端一點的就是完全負相關“相關係數為-1”。就是兩種資產相互是負向連動的:A基金跌,B基金也一定漲,同時漲跌幅相對稱。而且當A基金漲時,B基金也一定跌。太漂亮了,假若能找到這兩組資產就太好了,因為兩者組合後,完全都不會波動嘛,也就是標準差為0。因為A基金所有的波動,都被B基金給抵銷了。
看完了上面敘述,讀者應當可以感覺到,資產配置的精髓是兩組資產的相關係數,這數字決定了相互之間有多少機會會相互抵銷。相關係數是由-1到1之間的一個值,愈往+1靠,『恰巧』的機會少,相互抵銷機會愈小;愈往-1偏,『恰巧』的機會多,抵銷機會愈大。到了-1就是完美的組合了,因為可以完全抵銷風險。但是不要高興太早,在理財實務裡,要找到負相關的資產已經非常困難了,更別提完全負相關,這是不可能的事。
平均報酬不會相互抵銷
哇!太好了。波動可以相互抵銷,但通通抵銷掉了報酬不就沒了。不會的,所謂波動指的是平均值上下的波動,也就是平均值的離差和。波動相互抵銷後,所得到的就是穩定的平均值。對基金而言,會有一個平均報酬率以及標準差。平均報酬率就是平均值,標準差就是在平均報酬率上下波動的程度。所以當兩資產相互配置後,平均報酬率是不會改變的,但是標準差(風險)會變小。
美國股票及債券長期之相關係數為0.2
理論背景交待完畢,現在我們就可以輕鬆進入主題了。去瞧瞧由富達的研究機構MARE(Market Analysis, Research and
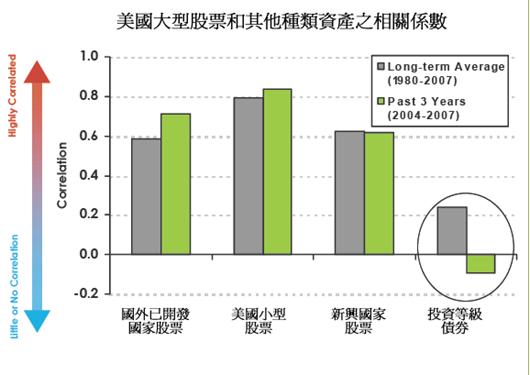
Education)所發表的文章講的是啥東西。其實這一篇主要是將過去的美國大型股票,和其他種類的資產類別的相關係數做了一些整理。灰色的長條代表約30年來的長期平均值,綠色部分是最近三年的數據。
這張圖也說明美國大型股票和小型股相關性一直都維持在0.8上下,連動性相當高的,這也難怪因為都是同一國家的股票嘛。但是和國外的已開發國家例如西歐北歐等,相關度就較小,維持約0.6的相關度。只是最近三年,相互的連動性似乎增加了。至於新興國家,以前跟最近一直都維持0.6的相關度。
從這張圖裡可以看到,美國大型股和其他類型股票的相關係數,最近三年來並沒有多大改變,但是債券部份卻變化很大,由以前的0.2變到約-0.1,這代表最近三年美國股票及投資等級債券相配合,是能有效消除波動風險的。
下面這張圖說明美國大型股票和債券型基金相互配置後的結果會是如何?水平軸代表的是風險(Risk)亦就是標準差,以百分比來表示;垂直軸是期望報酬率(%)。中間那條曲線就是用不同比例的混合,所得到的結果。
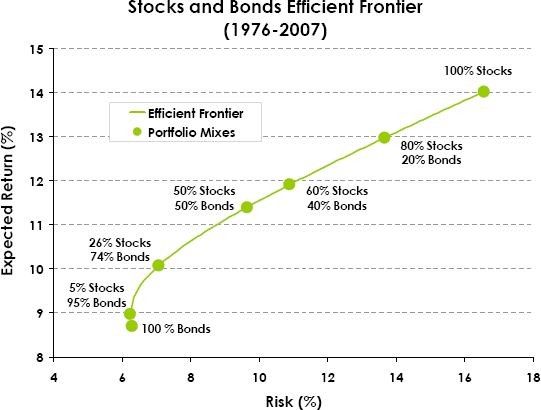
例如線最右上方那一點是整個組合百分百是股票,期望報酬率是14%,風險標準差約16.5%;最左下方那一點就是整個組合都是債券,期望報酬率是8.5%,風險標準差約6.2%,這兩點所形成的曲線是混合的結果。中間那一點(60% Stocks 40% Bonds),就是六成股票4成債券,期望報酬率是12%,風險標準差約11%。愈往右上面的點代表股票成分愈高,往左下的點代表債券成分愈高。可以看到這條線並不是直線,而是一條偏左上方微凸的曲線。
比較最左下方的兩點:一點是100%的債券沒有股票;另一點是95%債券,5%股票。你會發現有5%股票成分那一點,波動風險減少了可是預期報酬卻增加了。這代表雖然股票波動大,但只要比例對、配的對,不只是會增加報酬,同時還會降低風險的。
再往右上一點,股票部位增加約30%,期望報酬率由8.5%提升至約10.2%,可是風險只增加一點點約不到1%。我們只要順著這曲線就可找到自己適合的配置。這樣的配置選擇方式,就是資產配置的精髓。
結論
所以資產配置這一條曲線,愈往左上凸愈好。當兩資產的相關係數愈往-1靠時,這曲線就凸的更厲害。所以相關係數決定了資產配置的品質,下次當有理專跟你提出資產組合時,可不要忘了問這相關係數是多少。
經過這樣的解說,再配上基金公司的資料,相信對相關係數就會有著不同的看法。這裡頭的計算其實是非常繁雜的,所幸專業機構會幫我們做這一部份,做為個人投資者,我們只需要了解其意義,懂得閱讀專業機構所提出來的數據即可。
附註:兩組資產配置之數學
這裡只列出公式,欲知詳情請自行參考投資學及統計書籍。
有兩組資產其平均報酬率、標準差及資產比例如下表所示:
| 平均報酬率 (μ) |
標準差 (σ) |
資產比例 (w) |
|
| A資產(股票型基金) | μa = 14% |
σa = 17% |
wa = 0.5 |
| B資產(債券型基金) | μb = 8% |
σb = 6% |
wb = 0.5 |
| AB資產相關係數 |
ρab = 0.2 |
||
相配置後:
平均報酬率 = wa*μa + wb*μb = 0.5*14%+0.5*8% = 11 %
標準差 = ((wa*σa)2 + (wb*σb)2
+ 2 *ρab* wa*σa * wb*σb)1/2
Excel 表示 =
((0.5*17%)^2+(0.5*6%)^2+2*0.2*0.5*17%*0.5*6%)^0.5
= 9.6%
由上面的式子裡也可以看到,組合後平均報酬率和相關係數無關,但是標準差不只和相關係數息息相關,而且主宰整個標準差大小,亦就是波動風險。我們來看上面算式的結果,經過50%股票型基金50%債券型基金的配置後,組合後平均報酬率11%,風險調整為9.6%。如果同樣AB兩組基金,但是相關係數由0.2調整成-0.2。組合後平均報酬率還是11%,可是標準差卻縮小為:
= ((0.5*17%)^2+(0.5*6%)^2-2*0.2*0.5*17%*0.5*6%)^0.5 = 8.4%






