存續期間:債券價格波動之指標
日期:2013-02-23
投資債券屬於固定收益的一種,主要的獲利來自於債券的配息,所以理應是非常穩定的投資標的。持有債券就好像是把錢借出去,然後靠著收取利息來獲利是一樣的,只要配息及本金可以拿回來,沒有不會獲利的道理。雖說債券依賴配息獲利,但是因為債券的到期時間較長,本金及配息很久以後才拿得回來,所以債券的價值很容易就受到市場利率的變化而產生波動。
債券的存續期間(Duration),就是用來衡量市場利率的變化對債券價格的敏感度,一檔債券的存續期間愈長,就代表這檔債券對利率比較敏感,也就是只要市場利率稍有變化,就會造成債券價格較大的波動。存續期間較短,當然對市場利率的敏感度就會比較低。
存續期間的意義及應用
存續期間的單位雖然是年,但實際的意義確跟年數沒有直接關係,而是債券價格的變化率受殖利率影響的程度。實務上,修正後存續期間比較好用,只要將存續期間除上(1+殖利率),就可以得到修正後存續期間,就可以知道這檔債券受殖利率的影響會有多少。
舉例來說,一檔債券A在殖利率為6.5%的條件下,存續期間為-6.03。那麼修正後的存續期間 = -6.03 /(1+6.5%) = -5.66。也就是當殖利率上升1%時,債券的價格會下降5.66%。另一檔債券B,在同樣殖利率情況下,修正後存續期間若只有-3.2,那麼當殖利率上升1%時,債券的價格就只會下降3.2%。顯然,債券B的價格受到市場利率(殖利率)的影響較小。
所以,存續期間是用來衡量債券價格對殖利率敏感的程度,跟時間是沒有關連的。只要知道每一檔債券的存續期間,就可以知道那一檔債券的價格受到市場利率的影響比較大。而且影響的程度有多大,也可以用存續期間預估出來。
接著所要敘述的都是針對較為嚴謹的讀者,這族群若不完全了解存續期間的公式如何導出,是不會善罷干休的。文章中會使用到微分公式,難度較高、需要靜下心來慢慢細讀。對於存續期間的來龍去脈沒興趣的讀者,就直接跳過吧。只要了解存續期間的意義及應用就夠了,至於公式怎麼來的,不懂也不會影響投資績效的。
利率風險只在轉售時才發生
許多投資者對利率風險不是很了解,怎會利率變化造成投資損失呢? 既然持有債券等於把錢借出,那麼只要不被倒帳實在沒有虧錢的道理呀!以前的經驗告訴我們,將錢借給別人以收利息獲利,只擔心被倒帳而已,從來也沒有因為市場利率的變化而發生過虧損。
持有債券跟一般借貸又有何不同呢?為何市場利率波動會造成債券價值盈虧。這當中主要的區別,就是持有債券的期間允許債券轉讓(出售)。民間的借貸都是得持有到期滿,其間沒有債權轉售的問題,然而債券因為到期日都非常長,債券的持有者需要現金時,可以到債券市場轉售,這當中就會有利率風險出現。
其實即便是民間借貸,只要期中有轉售的行為,也會出現利率風險的狀況。舉個簡單的例子來說明,James借出100萬元給一家企業,雙方定下合約年利率5%、期間二年,無須抵押品,貸款期間並不付息,本息以複利計算,到期時一併償還。
如果James這兩年當中都不需要用這筆錢, James兩年後可以拿回本息1,102,500元 (=1000000*(1+5%)2 ), 計算方式請參考《複利完全攻略篇》,所獲得的報酬跟市場利率完全無關。
但是若James出借後突然家裡有急用,只好找Peter商量是否願意承接這債權。Peter是個精明商人,衡量當時銀行信用貸款的利率為8%,所以除非利率也是8%,才願意承接這筆債權,所以只願意支付945,216元 ( =1102500/(1+8%)2)。朋友中沒有人比Peter出更高的價錢,所以James只好用這價錢出讓。James借出100萬卻只收回了945,216元,這筆貸款損失了54,784元,這就是利率風險。因為當初以5%借出,轉讓時卻是8%,所以才會有損失。
再強調一次,利率風險只有在轉讓時才會出現。假若James持有這債權到期,其中不論利率是多少,都可以十足的拿回本息1,102,500元,所以就沒有利率風險問題。
債券的價值是未來現金流量之現值
想要了解利率波動對債券價值的影響,首先就得知道債券價值的計算方式。所有的投資商品其價值等於未來可以拿回之現金流量現值,當然債券也不例外。所以只要列出債券的現金流量,然後將這些現金流量的現值加總就是債券的價值了。
以上述James借貸的例子來說,雖然只是民間借貸,但性質上也屬於債券的範疇,當然也可以用現值來計算其價值。因為期中並不支付利息,所以未來只有一筆現金流量,就是兩年後的本利和1,102,500元。因為這筆金額是兩年後才拿得到,且Peter期望可以獲得8%的年利率,所以現值等於現金流量除上1/(1+8%)2,計算公式如下:
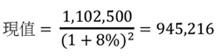
一般債券的現金流量就較為複雜了,通常是每期都可以收到利息,到期時再拿回本金,所以一檔債券的持有者,可以拿到的現金流量如下圖,第一年到第六年都是利息(c1~c6),第七年的現金流量是利息加上本金c7。
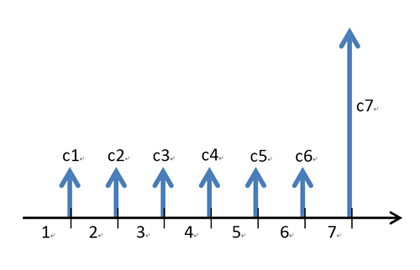
現金流量畫出來以後就簡單了, 若投資者要求之利率(市場利率)為y,那麼這檔債券的價值就是所有現金流量的現值加總(P),用公式表示如下:
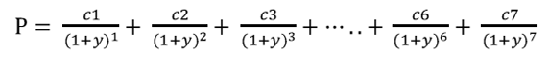 -----公式一
-----公式一
公式一說明了債券價格P是市場利率y的函數,當市場利率( y )變動時,債券價格P也會隨之變動。因為折現因子為1/(1+y)年數,所以年數愈長的現金流量,變動的幅度就會愈大。
存續期間是價格波動率與殖利率波動率之比例
只知道債券價格公式還不夠,若要得到市場利率對價格變動的影響,可以將債券價格(p)對(1+y)微分,就會得到下列式子:
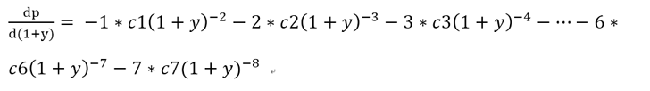
再將 上面等式的兩邊各別乘上(1+y)/p,就可以整理成下列的公式二。
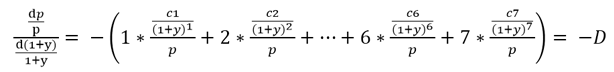 -----公式二
-----公式二
公式二的等號最左邊式子說明了存續期間的定義,中間式子所代表的是存續期間的計算方式,等號最右邊的D就是Duration的縮寫,負號說明了債券價格跟利率是反向的。
最左邊式子的分子dp/p就是債券價格的變化率,分母d(1+y)/(1+y)就是1+y的變化率,所以存續期間的意義是「價格的變化率」除上「1+y的變化率」,也就是說價格變化率是1+y變化率的多少倍。
實務上就直接將dp以Δp代替,d(1+y)用Δ(1+y)代替,就變成下列實用的公式三。因為存續期間D也是殖利率y的函數,所以不同的殖利率也會有不同的存續期間,所以在應用存續期間時,必須指定在甚麼殖利率的情況下才有意義。
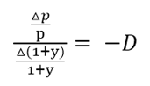 -----公式三
-----公式三如果將公式三的分母移到右邊,公式就更容易了解了。
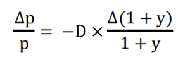
等式左邊的Δp/p就是價格變化率,也可以說是p點的投資報酬率。例如殖利率y時,用p的價格買入債券,當殖利率為y+Δy時,這時候的價格為p1,Δp就是(p1-p),也就是獲利,所以Δp除上p就是以p為基準的投資報酬率。因為1+y的變動跟y的變動是一樣的,所以Δ(1+y)=Δy,所以Δ(1+y)/(1+y) =Δy /(1+y)。
舉個簡單的例子來解釋,票面利率5%,七年到期之債券,當殖利率為6.5%時,價格為91.77,存續期間為-6.03。只要知道存續期間多少,我們就可以評估這檔債券對市場利率的影響,就是殖利率升高1.065%,債券價格會下跌6.03%。
***殖利率y為6.5%時,(1+y)就是1.065,(1+y)上升1%就等於殖利率上升1.065%。
修正後存續期間更實用
上述的例子雖然說明了存續期間的意義及應用,但總覺得繞了一圈不夠直接。雖然1+y的變化率對價格的變化率很重要,其實投資者更想知道殖利率的變化量(Δy),對價格變化率(Δp/p)的敏感程度。也就是殖利率每上升1%時,債券價格會變化多少。所以將公式三再整理一下,就可以得到公式四如下:
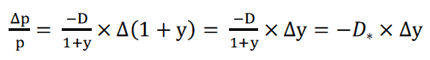 -----公式四
-----公式四
只要將存續期間D除上1+y之後,就是修正後存續期間D* (Modified Duration)。修正後存續期間可以知道債券價格變化率及殖利率變化量之比值。以上述同樣的例子來解釋,若想知道當殖利率在6.5%情況下,若上升0.25%及1%時,投資報酬率個別會降多少呢?
只要知道殖利率6.5%時的修正後存續期間D*就可以了。因為當殖利率6.5%時,存續期間為-6.03,所以D* = -6.03/(1+6.5%)= -5.66。所以殖利率每上升1%,債券價格就會跌5.66%。若殖利率只上升0.25%,債券價格就會跌1.415% (=-5.66*0.25%)。
驗算一下
以上敘述是用修正後存續期間的結果,用Excel的PV函數可以精確算出債券的價格,下表分別列出相同的現金流量,在三種不同的殖利率時的價格,看看是否吻合修正後存續期間的預估。
| 殖利率(y) | 價格(p) | Excel 公式 |
| 6.50% | 91.77 | =PV(6.50%,7,5,100) |
| 6.75% | 90.49 | =PV(6.75%,7,5,100) |
| 7.50% | 86.76 | =PV(7.50%,7,5,100) |
當殖利率由6.50%升到6.75%時 (Δy=0.25%),價格會由91.77跌到90.49元(Δp = -1.29),投資報酬率(Δp/p)等於-1.40% (=-1.29/91.77),跟用修正後存續期間所預估的只差一點點。
當殖利率由6.50%升到7.50%時(Δy=1.0%),價格由91.77跌到86.76元(Δp = -5.01),投資報酬率(Δp/p)等於-5.46% (=-5.01/91.77),跟修正後存續期間所預估的-5.66%差距就較大。因為存續期間的公式是用微分所導出,所以當殖利率的變化很小時才準確,但是用來評估殖利率對價格的變動程度是相當夠用的。
存續期間的單位是年
了解存續期間是用來衡量殖利率的變動對債券價格的敏感度,相信許多人不了解為何單位卻是用年來表示,只要詳細了解公式二,就可以知道了。下圖是公式二的意義:
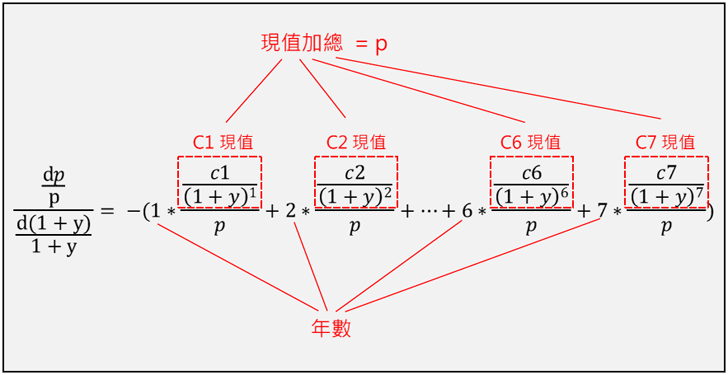
等式的右邊就是存續期間的計算方式,右邊的每一個加項,都是由年數乘上一個分數組合而成,其分母都是p也就是債券價格,分子就是該年度的現金流量的現值。例如C1/(1+y)1,就是第一年度現金流量C1的現值;C2/(1+y)2,就是第二年度現金流量C2的現值,依此類推。然而把所有年度的現金流量C1~C7的現值加起來,就是債券的價格p。那麼每一年的現金流量的現值(Cn/(1+y)n)除上p,就是該年度現金流量現值佔債券價格的比例。存續期間計算就是將每年度現值的比例乘上年數,也就是以年數做為加權平均的結果,其意義如下:
=-(1*第1年度現值的比例 + 2*第2年度現值的比例 + ….. + n*第n年度現值的比例)
得到的單位就是「年」,例如票面利率5%,7年到期的債券,得到的存續期間是-6.03年,負值代表債券價格的變動跟殖利率是反向的。
無息債券的存續期間就是到期年數
如果這是一檔無息債券,那麼因為期中不會配息,所以C1~C6都是零,現金流量只有最後以年C7,所以C7的現值就是債券價格,存續期間第7年的分子及分母一定相同,因為都是債券價格,存續期間就一定是7。所以可以得到一個結論,無息債券的存續期間跟該債券的到期年數是一樣的。
假若一檔無息債券還有6.03年到期,那麼該債券的存續期間就是6.03。所以一般的付息債券,不論多久以後到期,只要存續期間為6.03,也可以解釋為其對利率變動的敏感程度,相當於6.03年到期的無息債券。例如七年期、5%票面利率之債券,在殖利率為6.5%時,存續期間為 -6.03,所以其債券價格對殖利率的敏感度,跟6.03年後到期的無息債券是一樣的。
Excel輕易的計算出存續期間
存續期間要了解原理比較困難,只要用Excel來計算卻是易如反掌。提供一個存續期間Excel的試算表,可以幫助讀者學習之用,點選下列Excel圖示就可以下載。而且為了方便讀者與Excel上面的儲存格對照,以下括弧內的文字為儲存格位置。
首先當然要輸入債券的參數, 只要用票面利率(B1)及到期年數(B2),就可以描述出債券的現金流量(B欄第9列以後),因為存續期間跟殖利率相關,所以儲存格B3是輸入所要計算的殖利率,B4就是根據以上所輸入的參數所計算出來的債券價值。
計算方式就是在C欄列出每一年度的現金流量現值,因為B欄為現金流量,所以C欄就是根據同一列B欄的現金流量所計算出來的現值,債券價格(B4)就是這些現值的加總,也就是P的值。
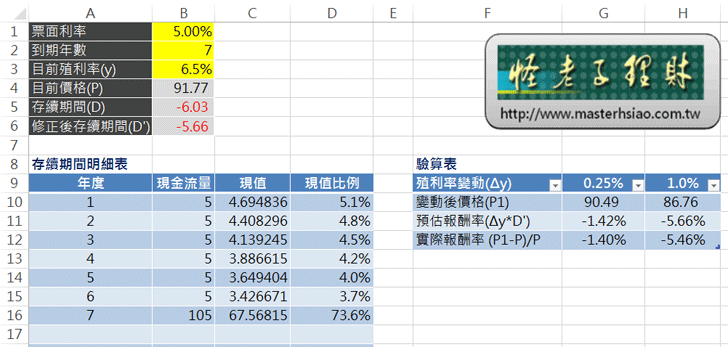
D欄就是同一列現金流量的現值佔債券價值B4的比例,例如第一年的現金流量5元,現值是4.694836元,佔債券價格91.77元的5.1%,依此類推。存續期間(B5)就是將每一列之現值比例(D欄)乘上年度(A欄),再加總起來的結果。以下圖為例,存續期間計算如下:
= -(1*5.1% + 2*4.8% + 3*4.5% + 4*4.2% + 5* 4.0% + 6*3.7% + 8*73.6%) = -6.03
修正後存續期間(B6)就是將存續期間(B5)再除上(1+y),
修正後存續期間 = -6.03/(1+6.5%) = -5.66%
下圖的驗算表(F9:H12)是當殖利率變動時,驗算實際報酬率及修正後存續期間預估值之差異。 當殖利率變動0.25%時,也就是殖利率由6.5%上升到6.75%,只要將0.25%乘上修正後存續期間-5.66,就可以知道價格會跌1.42%。實際上債券殖利率由6.50%上升至7.75%,債券價格就會由91.77 跌至90.49,跌幅為-1.40%,跟用修正後存續期間預估的差不多。當殖利率變動1%時,也就是由6.5%上升至7.5%,用修正後存續期間預估跌幅為-5.66%,實際上算出來卻是-5.46%,雖然差距較大但還是可參考。
好用的Excel試算表
試算表黃色的儲存格是使用者任意輸入的參數,其他儲存格都是計算出來的結果,不可任意變更。只要輸入票面利率及到期年數就可以描述一檔債券的現金流量,所以再輸入想計算存續期間的殖利率,試算表就會計算出存續期間以及修正後存續期間的值。不只如此,存續期間明細表也列出了計算明細。除此之外,右邊的驗算表計算當殖利率變動0.25%及1.0%時,比較修正後存續期間所預估的價格變化率,以及實際的價格變化率之差異。相信透過這個試算表,讀者就更容易了解存續期間的意思了。






