如何預估ETF未來報酬率
日期:2021-05-07
國內投信只要刊登ETF或基金的廣告,都被金管會要求列出「過去之績效亦不代表未來績效之保證」之警語,其實這句話不僅針對基金或ETF,也一併適用所有的金融資產。然而大部分的投資者把這警語當成耳邊風,都是看到哪個標的績效好,就就往那裏投資。金管會的警語雖然正確,但過去的績效是很重要的投資依據,怎麼可以不加以了解,只是不能只看一次的績效,而且要正確解讀才行。
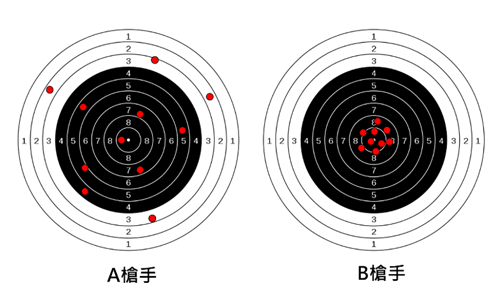
用打靶的例子說明會更清楚,每位射擊選手雖然都瞄準靶心,但是射擊出來的彈著點每一位都會不一樣,就像圖1中的A、B兩位選手,很明顯的選手B的準確度比較高,因為全部集中在靶心的部位,而選手A的彈著點卻比較稀疏。如果要量化兩位射擊手的準度,只要量測每一發偏離靶心的距離,加總起來除上射擊的發數,就是平均偏移的程度。平均偏移程度愈小,就代表愈準確。
如果射擊次數只有一次,就沒有辦法透過射擊結果判斷好壞,例如A選手的彈著點也有一發落在靶心附近,只是那次較幸運而已,其他時候就不是這樣。只要透過大量的射擊結果,除了可以判斷槍手好壞之外,還可以推估下次射擊彈著點可能的範圍。
圖一:B槍手射擊的準確度比較高
投資也是一樣,如果只看到過去一年投資報酬率30%,是無法就此認定這項資產品質好壞,也無法保證未來每年都會有這麼好的表現。但如果用好幾年的績效,就可以量化平均報酬率以及偏離平均報酬率的程度,藉以判斷金融資產的好壞,進而估算未來一年的報酬率可能出現的落點範圍。平均報酬率就好似射擊的靶心,每一年的報酬率就像彈著點,其道理都是一樣。
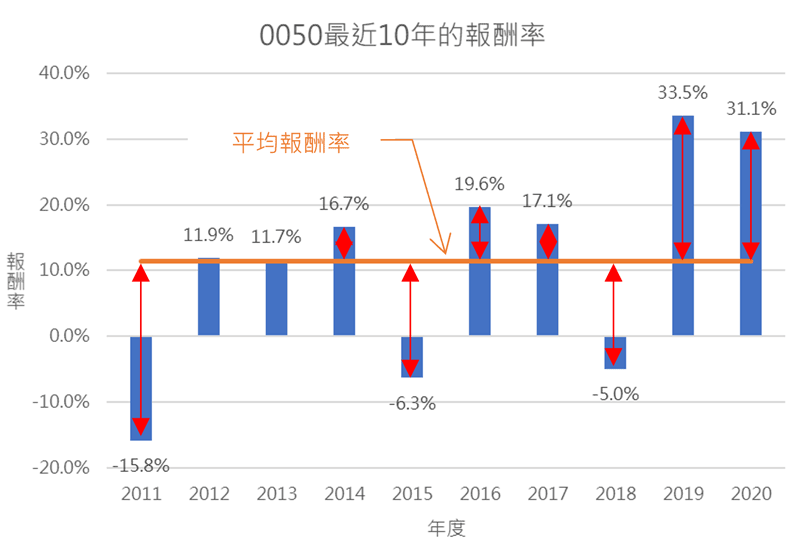
例如0050這檔ETF,在2020/3/12收盤價為82.15元,到了2021/3/12收盤價為135.25,一年的期間報酬率高達64.6%。這樣的績效,持有者當然很高興,但這一年的表現並無法保證是常態,有可能只是較幸運的一年。比較好的方式是將過去10年的年報酬率全部列出來(如圖2),求出平均報酬率以及偏離平均值程度,平均值就是將每一年報酬率加總除上10,算出來的結果為11.5%。偏離平均值的程度可以用統計的變異數來計算。變異數是將每一年報酬率減平均報酬率的平方,加總起來求取平均值,再將變異數的開平方根,就是標準差。實務上,波動風險的大小都是以標準差來表示。Excel提供一個標準差的函數STDEV.S,只要將每年報酬率代入即可,很方便就可以算出0050這10年的標準差為16.1%。
=STDEV.S(-15.8%, 11.9%, 11.7%, 16.7%, -6.3%, 19.6%, 17.1%, -5.0%, 33.5%, 31.1%)
=16.1%
知道平均每年報酬率11.5%,標準差16.1%,雖然說未來一年會有多少報酬率還是不曉得,但卻可以圈出一個範圍,根據機率的常態分配,有九成五的機率會落在平均報酬率正負兩個標準差之內,而平均報酬率加上兩個標準差就是43.7%(=11.5%+2*16.1%),平均值減掉兩個標準差就是-20.7%(=11.5%-2*16.1%),也就是說未來一年有95%的機率,報酬率落點為-20.7%~43.7%之間。
圖二:0050最近10年報酬率
用過去十年的報酬率來估算平均報酬及標準差,時間相隔太久遠,而且樣本數量只有10個,準確度就差了。實務上,都是採用最近3年的歷史月報酬率,以月初以及月底的收盤價為基礎,計算該月的報酬率。樣本採用最近3年也比較接近當前,而且樣本數也有36個,這樣得到的月平均報酬率及月標準差比較接近事實。再用月報酬率及月標準差推估年報酬率及年標準差。計算方式如下:
年報酬率 = 月報酬率*12
年標準差 = 月標準差*120.5 => Excel公式:=月標準差*SQRT(12)
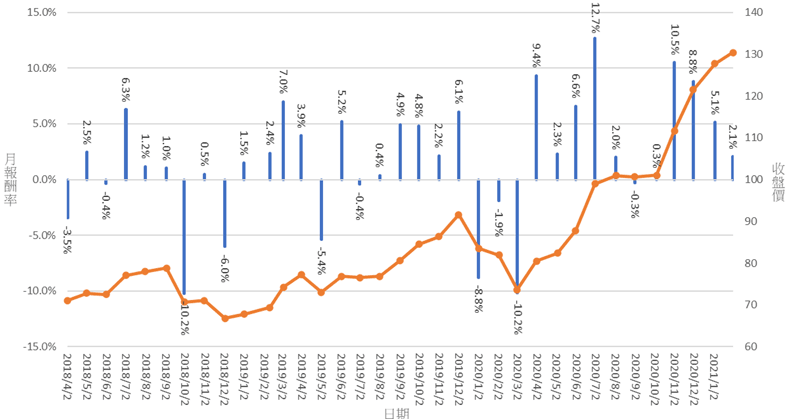
圖3就是以2018/4/2至2021/3/2日每月的報酬率及月初的收盤價,月平均報酬率為1.79%,月標準差為5.46%,換算成年報酬率為21.5%,標準差為18.9%。這樣的結果代表如果台股表現如過去3年,那麼未來一年的報酬率落點,有95%的機率會出現在年平均報酬率正負2個標準差之內,也就是-16.3%~59.3%,這好似可能的彈著點範圍很大,也就是風險很大的意思。
另一檔0056元大高股息ETF,於同一時期的年平均報酬率也有15.0%,標準差只比0050小一點點,也來到了18.3%,那麼未來一年報酬率可能的落點會在-21.6%及51.6%之間。從95%機率的落點來看,持有0050要比0056還要好,因為下跌時可能跌比較少,而上漲時的漲幅可能比較大。
另外再看大家喜歡的中華電定存股,在同時期中華電的平均年報酬率為3.74%,年標準差為6.1%,這樣的數值在未來一年95%的機率落點為-8.5%~15.9%,也就是說持有中華電的風險比0050還來得低,只是相對的報酬率也會比較低,這就是所謂的低風險低報酬。
一個系統的產出可以用平均值及標準差來描述,例如運動員可以看成一個系統,運動員的實力也可以用平均速度及標準差描述,一位百米跑者下一次的成績是多少,確定數值不知道,但有了平均速度及標準差的數據,就可以預估成績可能的範圍。好的運動選手除了平均秒速低之外,標準差也要低才行,否則未來的成績不確定性就會很高。只是,選手所擁有的平均速度及標準差並無法得知,只能採用過去的紀錄去推估,這樣當然會有誤差,但也沒有其他更好的辦法。
一項金融資產的報酬率可以看成一個系統,也可以用平均報酬率及標準差描述。金融資產也跟運動員一樣,系統真正的平均報酬率及標準差多少並不知道,也只能用歷史資料去估算,表一所得到的數據正是用這樣的方式估算出來的,即便會有誤差,但也是最好的評估方法了。
表一:0050、0056及中華電(2412) 於2018/4/2至2021/3/2的數據
| 證券代號 | 年平均報酬率 | 年標準差 | 95%機率範圍 | 夏普比率 |
|---|---|---|---|---|
| 0050 | 21.5% | 18.9% | -16.3%~59.3% | 1.14 |
| 0056 | 15.0% | 18.3% | -21.6%~51.6% | 0.82 |
| 2412(中華電) | 3.7% | 6.1% | -8.5%~15.9% | 0.61 |
圖3:0050月收盤價及月報酬率分布