EXCEL財務函數IRR、XIRR、MIRR
日期:2009-06-25
IRR(Internal Rate of Return)稱為內部報酬率,其應用非常廣大,是學習財務管理不可或缺的工具。Excel也提供了一個相對函數IRR 來呼應。本篇也包含IRR相關的其他兩個函數XIRR以及MIRR,讓讀者可以清楚知道每個函數的應用時機。
現金流量(Cash Flow)
閱讀本篇之前讀者必須先了解現金流量,才會知道IRR的意義。對現金流量還不了解的讀者,怪老子網站的『現金流量』篇有詳細介紹。
IRR函數
一個投資案會產生一序列的現金流量,IRR簡單說:就是由這一序列的現金流量中,反推一個投資案的內部報酬率。
如何反推呢,所用的方法是將每筆現金流量以利率rate折現,然後令所有現金流量的淨現值(NPV)等於零。若C0、C1、C2、C3...Cn分別代表為期初到n期的現金流量,正值代表現金流入,負值代表現金流出。
0 = C0 + C1/(1+rate)1 + C2/(1+rate)2 + C3/(1+rate)3....+ Cn/(1+rate)n
找出符合這方程式的rate,就稱為內部報酬率。問題是這方程式無法直接解出rate,必須靠電腦程式去找。這個內部報酬率又和銀行所提供的利率是一樣的意思。
IRR函數的參數定義如下:
=IRR(Values, guess)
| 參數 |
意義 |
必要參數 |
| Values | 現金流量 | 必要 |
| guess | 猜測IRR可能的落點 | 選項 |
IRR的參數有兩個,一個是Values也就是『一序列』現金流量;另一個就是猜個IRR最可能的落點。那麼Value的值又該如何輸入?有兩種方式可輸入一序列的現金流量:
- 使用陣列:例如=IRR({-100, 7, 107}),每一個數字代表一期的淨現金流量。
- 儲存格的範圍:例如=IRR(B2:B4),範圍中每一儲存格代表一期

那麼
=IRR({-100, 7, 107}) 或
=IRR(B2:B4)
都會得到同樣答案:7%
使用者定義期間長短
IRR的參數並沒有絕對日期,只有『一期』的觀念。每一期可以是一年、一個月或一天,隨著使用者自行定義。如果每一格是代表一個『月』的現金流量,那麼傳回的報酬率就是『月報酬率』;如果每一格是代表一個『年』的現金流量,那麼傳回的報酬率就是『年報酬率』。
例如{-100, 7, 107}陣列有3個數值,敘述著第0期(期初)拿出100元,第1期拿回7元,第2期拿回107元。第一個數值代表0期,也是期初的意思。至於每一期是多久,使用者自己清楚,IRR並不需要知道,因為IRR傳回的是『一期的利率』。當然如果使用月報酬率,要轉換成年報酬率就得乘上12了。
一年為一期
例如期初拿出100元存銀行,1年後拿到利息7元,2年後拿到本利和107元,那麼現金流量是{-100, 7, 107}。很清楚的這現金流量的每期間隔是『一年』,所以=IRR({-100, 7, 107}) = 7%傳回的就是『年報酬率』。
一個月為一期
換個高利貸公司的例子來看,期初借出100元,1個月後拿到利息7元,2個月拿到本利和107元,整個現金流量還是{-100, 7, 107}喔,不一樣的是每期間隔是『一個月』。那麼IRR傳回的 7%就是『月報酬率』,年報酬率必須再乘上12,得到84%的年化報酬率。所以每一期是多久只有使用者知道,對IRR而言只是傳回『每期』的報酬率。
guess-猜測報酬率可能的落點
guess真是個有趣的參數,IRR函數的任務不就是要解出報酬率的值嗎,怎會要我們自己猜測報酬率的落點呢?這不是很奇怪嗎,Excel計算功能那麼強,難道IRR函數無法直接解出來?沒錯IRR是無法解的。以{-100, -102, -104, -106, 450}這現金流量為例,等於得求出下列方程式中rate的解:
0 = -100 -102/(1+rate)1 -104/(1+rate)2 -106/(1+rate)3 + 450/(1+rate)4
這就難了!因為有4次方。假若現金流量的期數更多,那就更複雜了,而且使用者會輸入幾期還不知道哩。還好雖然無法直接求解,Excel使用代入逼近法,先假設一個可能的rate(10%),然後代入上面式子看看是否吻合,如果不是就變動rate的值,然後慢慢逼近、反覆計算,直到誤差小於 0.00001% 為止。如果真正的解和預設值差距過遠,運算超過20次還是無法求得答案,IRR 函數會傳回錯誤值 #NUM!。這時使用者就必須使用較接近的 guess 值,然後再試一次。
所以guess參數只是IRR函數開始尋找答案的起始點而已,跟找到的答案是無關。下面三個IRR公式,同樣的現金流量,但是guess參數都不同,結果答案卻都一樣是3.60%。
=IRR({-100, -102, -104, -106, 450})
=IRR({-100, -102, -104, -106, 450}, 1%)
=IRR({-100, -102, -104, -106, 450}, 2%)
guess是選項參數
guess參數可以省略不輸入,這時Excel會使用預設值10%。通常這是一年為一期報酬率都落在這附近,如果要計算月報酬率最好輸入1%,依此類推。
XIRR函數
若要利用IRR函數來計算報酬率,現金流量必須是以『一期』為單位,也就是輸入的現金流量必須有期數的觀念。但是常常有些應用,現金流量並非定期式的。例如一個投資案,現金流量如下表:
日期 |
金額 |
| 2007/8/15 | -100,000 |
| 2007/11/6 | 23,650 |
| 2008/3/4 | 25,000 |
| 2009/6/8 | 82,500 |
可以看到現金流量發生日期是不定期的,並非以一期為單位。XIRR就是專為這類型的現金流量求報酬率,其他觀念和IRR函數沒有差別。XIRR傳回來的報酬率已經是年報酬率。
XIRR參數
XIRR(values, dates, guess)
| 參數 |
意義 |
必要參數 |
| Values | 現金流量的值 | 必要 |
| dates | 現金流量發生日期 | 必要 |
| guess | 猜測XIRR可能的落點 | 選項 |
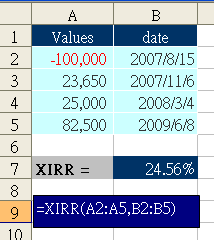
和IRR函數的差別是多了一個日期(dates)參數,此日期參數(dates)必須跟現金流量(Value)成對。例如上面的例子可以如下圖的方式來完成。儲存格B7的公式 =XIRR(A2:A5,B2:B5),算出來這投資案相當於每年24.56%的報酬率。
需要開啟分析工具箱
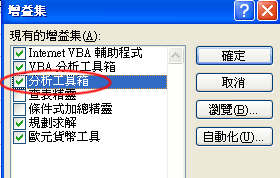
使用XIRR函數必須安裝「分析工具箱」,否則會傳回#NAME? 錯誤。
1) 工具/增益集
2) 將分析工具箱打勾
3) 按確定
MIRR函數
MIRR參數
MIRR(values, finance_rate, reinvest_rate)
| 參數 |
意義 |
必要參數 |
| values | 現金流量的值 | 必要 |
| finance_rate | 融資利率 | 必要 |
| reinvest_rate | 再投資報酬率 | 必要 |
MIRR是Modified Internal Rate of Return的縮寫,意思是改良式的IRR。IRR到底有何缺點,需要去修正呢?主要的原因是IRR並未考慮期間領回現金再投資問題!IRR的現金流量裡可分為正值及負值兩大類,正值部分屬於投資期中投資者拿回去的現金,這些期中拿回去的現金該如何運用,會影響報酬率的。負值部分屬於投資期中額外再投入的資金,這些資金的取得也有融資利率方面要考慮。
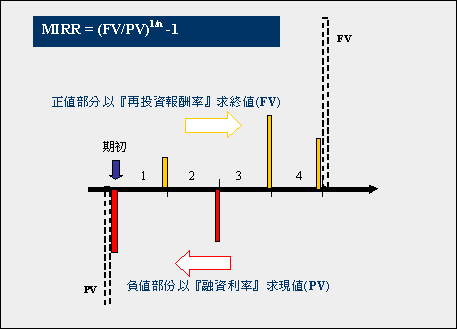
MIRR使用的方式是將期間所有的現金流入,全部以『再投資利率』計算終值FV。期間所有的現金流出,全部以『融資利率』計算現值PV。那麼MIRR的報酬率:
=(FV/PV)1/n - 1
再投資報酬率
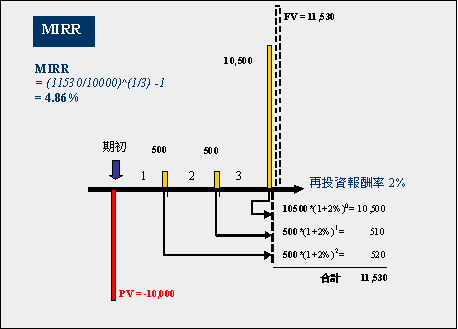
以例子來解說會較為清楚,一個投資案的現金流量如下:{-10000, 500, 500, 10500}這現金流量一期為一年,期初拿出10,000元,第1年底拿回500元,第2年底也拿回500元,第3年底拿回10500元。將現金流量代入IRR求內部報酬率:
=IRR({-10000, 500, 500, 10500}) = 5%
從這投資案的經營者來說,期初拿到10,000元,然後每年支付5%報酬500元,到了第3年底還本10000元,這投資案確實是每年發放5%的報酬沒錯。可是若從投資者角度來看,假若每年底拿到的500元只會放定存2%,也就是投資者期中拿回來的金額,到期末只有2%的報酬率,那麼投資者到第3年底時,實際拿到的總金額為:
= 500*(1+2%) + 500*(1+2%)2
+10500 ( 以Excel 表示 =500*(1+2%)+500*(1+2%)^2 + 10500
)
= 11,530
期初拿出10,000元,3年後拿回11,530,這樣相當於年化報酬率:
= (11530/10000)1/3-1 (Excel 表示
=(11530/10000)^(1/3)-1 )
= 4.86%
這可解讀為拿出10,000元,以複利4.86%成長,3年後會拿回11,530元。
MIRR可以不用那麼麻煩,只需輸入再投資報酬率2%,便可輕易得到實際報酬率:
= MIRR(({-10000, 500, 500, 10500}), 0, 2%)
= 4.86%
投資者期間內所拿回的現金(正值),再投資的報酬率,會影響整體投資的實際報酬率。同一個例子,假若另一位投資者的再投資報酬率為4%,那麼實際報酬率修正為:
= MIRR(({-10000, 500, 500, 10500}), 0, 4%)
= 4.95%
如果投資者的再投資報酬率為5%,實際報酬率等於:
= MIRR(({-10000, 500, 500, 10500}), 0, 5%)
= 5.00%
可以看到當再投資報酬率為5%時,MIRR = IRR = 5%。這也同時說明了,IRR內部報酬率是假設再投資報酬率等於內部報酬率。
融資利率
如果有第0期以外的現金投入(負現金流量),這些資金是在未來的期數才會使用。只要在期初準備這些資金的現值。就足以支付未來的這些金額。所以將所有的現金流出均以『融資利率』折現(PV),代表未來所有的投資額,都相當於期初投資PV的金額。
舉個例子:一個儲蓄險,頭兩年、年初繳保費5萬元。第二年底開始,往後四年均領回30,000元,若再投資利率為3%,融資利率為5%,求MIRR為多少?
= MIRR({-50000, -50000, 30000, 30000, 30000, 30000}, 5%,
3%)
= 5.15%
這是利率MIRR函數直接套入公式算出來的,為了解其中道理,將這些正負現金流量分開來,以分解動作求取終值及現值,再算投資報酬率。這樣讀者就很清楚MIRR是如何計算的。
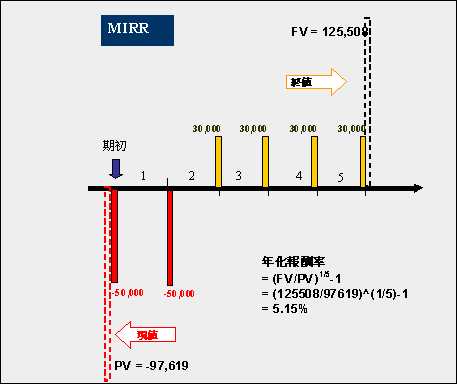
總共有兩筆現金流出(負值部份),但是只有第2期的資金流出需要折現,所以用『融資利率』5%,總現值(PV):
=50000 + 50000/(1+5%)
=97,619
這意思是說:若融資利率為5%,只需要在期初準備97,619,就足以支付前兩期各5萬所需的現金支出。
總共有4筆現金流入(正值部份),以『再投資利率』為3%,求取所有現金流入的終值(FV)
= 30000 + 30000*(1+3%) + 30000*(1+3%)^2 +
30000*(1+3%)^3
=125,508
那麼期初投入97,619,期末拿回125,508,期間為5年,這樣的年化投資報酬率:
= (125508/97619)^(1/5)-1
= 5.15%
可以看到和直接用MIRR函數所計算出來的報酬率一模一樣都是5.15%。
『融資利率』是微軟的說明所使用的名詞,我認為較為適當的應該是『資金報酬率』(finance_rate),也就是資金存放標的之報酬率。