每個人都希望當個有錢人，但是如果方法不對，可是一輩子無法富裕，只能平凡的過日子。這裡要告訴讀者，為什麼只有靠投資理財，才有機會晉升到有錢人的行列，也才有可能早日達到財務自由的目標。

唯有理財才可能致富

理財就是個人的財務管理，將已擁有的財富做最有效率的運用及管理。如果不懂得理財，這輩子大概就跟財富無緣。有這麼嚴重嗎，不會理財真的就沒辦法富有嗎？

不會理財有多悲慘

是的！如果不會理財，就只能靠工作亦就是薪資來賺錢。把一生中所賺得的薪資扣除花費外，通通加起來就是積蓄了。簡單算，如果一個家庭每年可以結餘50萬元，25歲開始工作，55歲退休，大概有30年的時間可工作，那麼到退休時的金額是1,500萬元！如果將通貨膨脹考慮下去，以每年2.5%的通貨膨脹率，相當於=PV(2.5%, 30, 0, 15000000) = 7,151,140。天呀！連續30年，每年都能夠有50萬元結餘喔，竟然會落到退休時只有約等值現金貨幣700萬的積蓄，連個台北市的房子都買不起。

注：本文的藍色斜體字是Excel財務函數，均可以直接複製到Excel的儲存格運算。FV為終值(未來值)函數，PV現值函數。函數的詳細說明請參考『Excel投資理財之應用』一文。

定存也只是聊勝於無

我想沒有人那麼笨，只會把賺來的錢藏在床底下，至少也會用定期存款來理財。如果以現今定存利率2.5%來看，每年50萬，30年結果又會是如何：

=FV(2.5%, 30, -500000) = 21,951,352

考慮通貨膨脹後：

=PV(2.5%, 30, 0, 21951352) = 10,465,146

嗯，還不錯，已經由700萬變成1,000萬了。買個房子大概沒問題，可是想要退休養老，恐怕就不太夠了。談到這兒，其實我很訝異國人在民國96年的調查中竟然有56.6%的比例是只有以定期存款來理財的。

看看會理財的人

如果會理財的人，每年可以有15%的投資報酬率，其他條件一樣，瞧瞧結果又會是如何呢：

=FV(15%, 30, -500000) = 217,372,573

考慮通貨膨脹後

=PV(2.5%, 30, 0, 217372573) = 103,630,784

不要以為你數錯了，也不是筆誤，確實是考慮通貨膨脹後還值一億元，整整是定存族的10倍之多。這就是為什麼，薪水可以決定能否吃得飽，然而理財卻決定了一生是否富有。

15%報酬率可能嗎

相信許多讀者心中已經憤憤不平，那有那麼好的事，大家又不是笨蛋，如果每年真有穩定15%的報酬率，又何必得放定存！一定又是投資股票或是基金的，那可是得承擔很大風險，不要到時弄得血本無歸、欲哭無淚，將來連個老本都沒有喔！這就是定存族內心所吶喊的聲音。

沒錯，就只有股票或基金能有這麼大的報酬，而且相對的有某種程度的風險存在。風險與報酬是位於天平的兩端，是對等的。想要有高報酬，就必須勇於承擔風險。可是風險真的有那麼可怕嗎，難道說都沒有方法可以有效管理風險嗎？有沒有什麼辦法可以讓我們在風險與報酬中得到折衷？當然有，整本投資學所談的就是這些。

風險有很多種，但是威脅最大的是：選錯標的風險以及波動風險。選錯標的風險可以透過購買指數型基金或者是ETF來解決，波動風險也可以透過長期持有策略來化解，畢竟股票或債券市場是長期看漲的。這部份可以參考網站『ETF淺談』及『為什麼長期投資股票一定賺』兩篇文章。

我不主張於尚未充分了解如何管理風險的情況，就進行高風險的投資行為。相反的，我認為投資者應該積極學習什麼是風險，了解衡量風險的方法，進而評估自己是否有能力承擔這風險。當一切風險大小都在掌握之中時，面對風險時自然就不畏懼了。

報酬率決定一切

由前面的例子可以看出，報酬率決定了一切。但是為何報酬率有這麼重大的影響？最主要原因就是有了複利的存在。

複利的威力無窮

貨幣是有時間價值的，在財務的世界裡，全部都是以複利方式來計算的。不論銀行定存、房屋貸款、汽車貸款以及債券價格都是以複利為基礎。複利的意思是每一期末時，將當期所產生的利息再加上當期的本金，作為下一期的期初本金繼續升息。若第一期初本金為PV，每期利率為R：

當期所產生的利息是當期的期初本金乘上每期利率R，也就是每一期的期末本利和等於當期的期初本金乘上(1+R)。由上表的演算過程，可以看出第n期的終值和第一期本金PV的關係如下：

FV = PV*(1+R)ⁿ

由這公式可以看出本金以‘1+R’的n次方成長，n為期數。就是每增加一期，終值就會增加上一期終值的‘1+R’倍。所以說當期數愈多時，因為累積金額就愈大，每乘上一次‘1+R’可都不是個小數目。

下圖是以1萬元為本金PV，在不同利率R及年數n的終值圖。

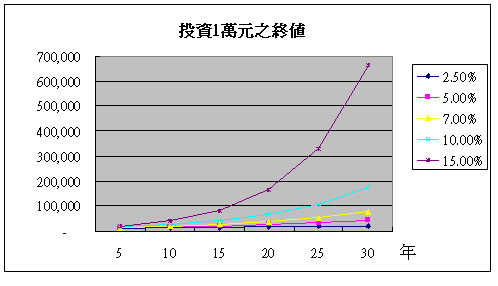
可以看出整個終值是以指數型態往上升的，報酬率愈高彎曲度愈陡，亦就是說愈到後面，每增加一年所升高的終值就愈高。這一點利用72法則來解釋會更明白。

奇妙的72法則

上面的公式及圖表以Excel計算是很容易的，但是對理財觀念的了解還是有限。有一個很有用的方法稱為72法則：用72這數字除上年利率R，所得的數字是：多少年的時間會使本金以複利成長一倍。例如年利率10%，那麼本金以複利增加一倍所需要的時間為72/10 = 7.2年。也可以這麼說，若投資本金1萬元於年利率10%的標的，以複利計算的話約7.2年會成長一倍至2萬元。使用72法則時，年利率R是要乘上100的，簡單的方法是省掉百分比“%”符號不要看。例如年利率7%，是以7當除數(72 / 7)，而不是用0.07來除(72 / 0.07)。

下表的中間那一欄是以72法則所計算的數字，就是每增加一倍本金所需要的年數。最右邊那一欄是以精確公式計算出的，可以看出72法則不用對數運算，只需簡單除法也可以得到蠻接近的值，確實是蠻實用的。精確值公式說明於附註。

報酬率 ( R )	72法則 =72 / (R*100)	精確值 =ln(2) / ln(1+R)
2.5%	28.8	28.1
5.0%	14.4	14.2
7.0%	10.3	10.2
10.0%	7.2	7.3
15.0%	4.8	5.0
20.0%	3.6	3.8

這72法則透露了一個很重要的訊息，就是：報酬率提高時，本金增加一倍的年數便大幅縮短了。當報酬率為2.5%時，本金得28年才會翻一倍。若報酬率增至15%時，只需約5年就會翻一番了。也可以這麼說：1塊錢的本金，2.5%報酬率要28年才會變成2元。但是15%的報酬率第5年就是2元了，再過5年(第十年)可不是只增加1元變成3元喔，而是2元的一倍成為4元，依此類推如下表：

時間(年)	1元的終值
0	1
5	1*2 = 2
10	2*2 = 4
15	4*2 = 8
20	8*2 = 16
25	16*2 = 32
28.3	52

這說明了什麼呢？同樣是本金1元，當2.5%報酬率以緩慢的速度成長，花了28年時間才漲到一倍(2元)，然而同時期15%的報酬率已經成長至52元了。哇！怎麼差那麼多呀。我們再看看前5年只不過增加1元而已，可是第20年到25年的這5年卻一口氣增加了16元。這是因為到第20年時，已經累積到了16元，所以從20年起的第5年就會賺16元。這代表了什麼，就是每5年會成長以前所累積的金額的一倍。這麼說好了，如果本金是100萬，到了第20年時已經成長16倍(1,600萬)，那麼只要再5年就會再增加一倍1,600萬成為3,200萬。聰明的讀者，相信已經知道再5年後會增加3,200萬成為6,400萬了。這就是複利的威力所在！只要報酬率夠高，可以在很短的時間內，賺到一輩子所累積的錢。

說一個我自己親身的故事給讀者分享，有一次和一位親戚閒聊，他很自豪的說年輕時兩手空空，到現在(約70歲)好不容易有了1,000萬存款。我跟他說如果會理財，是可以在5~10年內用這1,000萬賺到另一個1,000萬的。當時我預設7%~15%的報酬率，用72法則可以輕易算出是5~10年。這位長輩非常的不以為然，認為我信口雌黃隨便說說，想說他辛苦一輩子才能賺到的，我如何在這麼短時間內可以達成。可是在資本主義下，以錢賺錢就是這麼回事。如果有一億元，也可以賺到一億元，更不用說是1,000萬了。現在知道為何有錢人會愈來愈有錢了吧！

年紀愈大，威力愈大

從72法則裡，了解到只要報酬率高，可以在短時間賺取一倍的獲利，但這對年輕人效益並不是很顯著。因為年輕能投資的金額不大，通常薪水所能賺到的金額會遠比投資獲利還要多很多。所以即使5年一倍的獲利，絕對獲利金額比起薪資還是很少。但是到中年之後，通常積蓄會累積到一定的程度，投資理財的報酬可是非常驚人，甚至年報酬會比薪資還要多。例如1,000萬的10%就是100萬了，不會比年薪百萬差吧。

我並無意要年輕人不要投資理財，雖然絕對報酬比起薪資少，但是累積金錢的速度還是比別人快很多的。我想表達的其實是：年輕時的重點是工作賺錢，年老的重點是理財賺錢。而且我更要突顯當年紀愈大時，因為可投資的金額就大，效果更是顯著，這不正就是退休族所追求的目標嗎。

年輕時可以靠工作來賺錢，可是當年紀愈來愈老時，身體狀況便不再允許了。如果不會理財，不會用錢賺錢，也就只能靠省吃儉用來減緩積蓄的耗盡。可是反觀會用錢來賺錢的人，年老時不但不用工作，投資所賺的錢可不比年輕工作時少，而且隨著時間拉長可是愈賺愈多。我常很自豪的說，當我旅遊巴黎時，悠閒的在塞納河的左岸喝著咖啡，我的錢還是很努力的在幫我賺錢的。

結論

想成為有錢人唯一的方式是透過投資較高報酬率的商品，但是高報酬所伴隨的是高風險，只要做好資產配置以及風險管理，一切還是可以在掌握之中的。心中除了不會畏懼承擔風險外，還可以早日達到財務自由的目標。

附註：

精確計算本金翻一倍時的年數

終值和現值的公式如下

FV = PV*(1+R)ⁿ

我們希望知道當FV = 2*PV亦就是FV/PV = 2時，報酬率R和n的關係。

將上式等號的雙邊都除以PV，得到：

FV/PV = (1+R)ⁿ

再代入FV/PV = 2

2 = (1+R)ⁿ

等號兩邊各取自然對數

ln(2) = ln(1+R)ⁿ = n*ln(1+R)

所以以報酬率R要將本金翻一倍的年數n公式：

n = ln(2) / ln(1+R)